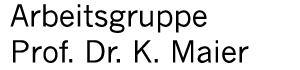Berechnen von Positronenannihilationsparametern
Um Positronenannihilationsparameter berechnen zu können macht man sich die Dichte-Funktional-Theorie (DFT) zu Nutze.
Die Dichte-Funktional-Theorie
1964 behandelten Hohenberg und Kohn (P. Hohenberg, W. Kohn, Phys. Rev. 136 (1964) 864) in einer Arbeit die Grundzustandsenergie eines inhomogenen Elektronengases. Sie bewiesen, dass die Grundzustandsenergie eines Elektronengases ein eindeutiges Funktional der Elektronendichte ist. Dies lässt sich schreiben als:
Hierbei ist V(r) das externe Potential und F[n(r)] das Funktional der Dichte. Das Mimimum der Energie liefert die korrekte Grundzustandsenergie zu dem Potenzial V(r). Kohn und Sham erweiterten diese von Hohenberg und Kohn entwickelte Methode zur Behandlung eines inhomogenen Elektronengases von wechselwirkenden Elektronen
(W. Kohn, L. J. Sham, Phys. Rev. 140, A1133, 1995.)Dies bedeutet für Berechnung der Energie wird eine geschätzte Dichte n(r) angenommen. Mit dieser Dichte wird die Energie bestimmt. Im Minimum der Energie ergibt sich eine neue Dichte n(r), die wiederum für einen neuen Zyklus der Berechnung der Energie eingesetzt wird. Diese iterative, und rechenintensive Methode liefert schlussendlich die gesuchte Dichte.
Dichte Approximation
Die Lokale Dichte Approximation ist die einfachste Methode die Austausch-Korrelations Energie in einem Elektronen-System zu beschreiben. Bei der LDA wird der Einfachheit halber angenommen, dass die Austausch-Korrelations-Energie Exc eines zu betrachtenden Elektronengases mit der Dichten n(r) an dem Punkt r identisch ist mit der Austausch-Korrelations-Energie eines homogenen Elektronengases der selben Dichte, an der zu untersuchenden Stelle r. Die Austausch-Korrelations- Energie Exc lässt sich schreiben als:
Hierbei ist exc die Austausch-Korrelationsenergie der des einzelnen Teilchens und n die Dichte. Eine Weiterentwicklung der LDA ist die Genaralisierte Gradienten Approximation (GGA). Bei dieser Approximation wird der Gradient der Ladungsverteilung an der Stelle r mit in Betracht gezogen.
Zusammenhang von Elektronendichte und Positronenannhilationsparameter
Die Lebensdauer eines Positrons τ ist eine Funktion der Elektronendichte. Dies bedeutet für Positronen, die in Leerstellen eingefangen sind, dass dort, aufgrund der geringeren Dichte von Elektronen im Gegensatz zum Zwischengitterbereich, die Lebensdauer erhöht sein wird. Die Annihiliations-Rate λ ist durch den Überlapp von Positronen-Dichte n+(r)=|ψ+(r)|2 und der Elektronen-Dichte n-(r) gegeben:
Annihilationsparameter des Aluminium Gitter
Mit Hilfe der von Kohn und Sham entwickelten Dichte-Funktional-Theorie (DFT) wird die eletronische Grundzustandsenergie des Gitters berechnet. Sie besagt, dass die Minimumsenergie eines Eletronensystems ein eindeutiges Funktional der Elektronendichte ist. Hat man die Minimumsenergie des zu untersuchenden Systemes gefunden, so folgt hieraus die Elektronendichte. Diese steht im direkten Zusammenhang mit der Lebensdauer der Positronen. Je höher die Elektronendichte im Gitter ist um so kürzer ist die Positronenlebensdauer in diesem Gitter. Das Positron annihiliert früher mit einem Elektron als dies in einem Gitter geringerer Elektroendichte der Fall ist.
Das Ergebnis der Berechnungen liefert mit einem Wert der Positronenlebensdauer im ungestörten Al-Gitter τb = 168 ps.
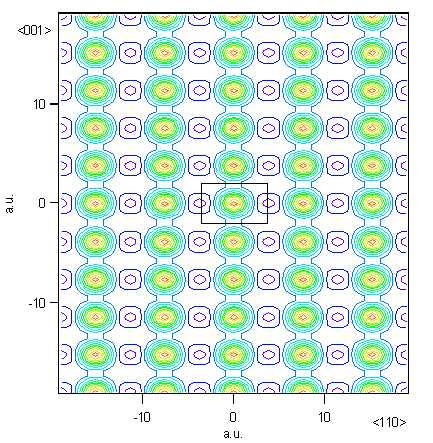
Entfernt man aus dem Alumium Gitter ein Atom, so entsteht eine Fehlstelle. Diese Fehlstelle bildet ein attraktives Potential für die Positronen. Diese werden in dem entstandenen Potentialtopf gebunden. Hierdurch erhöht sich die Positronenlebensdauer τv = 240 ps.